Aが36度の二等辺三角形、残りの角度は?
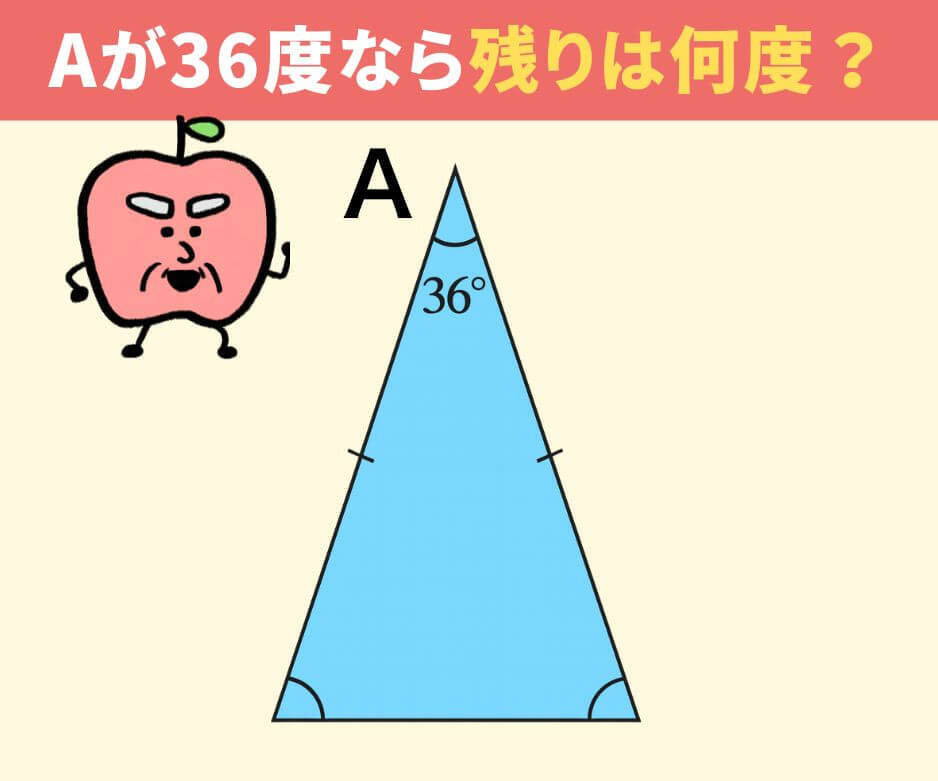
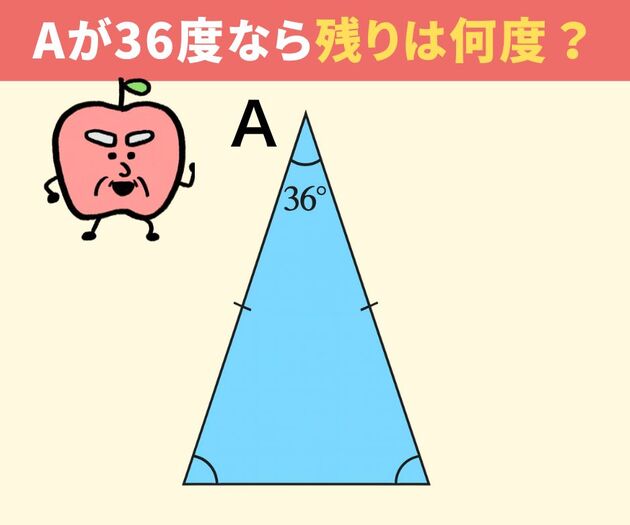
二等辺三角形があります。
頂角Aの角度:36度
この二等辺三角形の残りの2つの角(底角)は、それぞれ何度でしょうか?

正解は…

「72度」が正解でした!
頂点が36度の二等辺三角形の底角は、それぞれ72度になります。
なぜ72度になるの?
つい「えーっと、どう計算するんだっけ?」と迷ってしまいますが、実は2つの基本ルールを使うだけで簡単に解けるんです。
三角形の内角の和は180度
まず大前提として、どんな三角形でも「内角の合計は必ず180度」というルールがあります。これは小学5年生で習う基本中の基本ですね。

二等辺三角形は「2つの底角が等しい」
二等辺三角形には特別な性質があります。それは「2辺の長さが等しい三角形では、その2辺に向かい合う角度も等しい」ということ。つまり、底角の2つは必ず同じ角度なのです。
計算してみよう
この2つのルールを使えば、簡単に答えが出せます。
手順① 三角形の内角の和から頂角を引く
180度 - 36度 = 144度
これが「残りの2つの角の合計」です。
手順② 2つの底角は等しいので、2で割る
144度 ÷ 2 = 72度

つまり、それぞれの底角は72度ということになります!
【豆知識】いろんな二等辺三角形で使える公式
この考え方は、どんな二等辺三角形でも使えます。
底角の求め方 = (180度 - 頂角)÷ 2
例えば、
・頂角が40度なら → (180 - 40)÷ 2 = 70度
・頂角が50度なら → (180 - 50)÷ 2 = 65度
・頂角が80度なら → (180 - 80)÷ 2 = 50度
逆に、底角から頂角を求めることもできます。
頂角の求め方 = 180度 - (底角 × 2)
例えば: - 底角が60度なら → 180 - (60 × 2) = 60度(正三角形!)
実は小学校5年生の問題でした!
二等辺三角形の角度問題は小学5年生で学習する内容。子どもに質問されたときにサッと答えられたら、ちょっとカッコいいかもしれませんね!
果たして、正解がわかったでしょうか?もし間違えた場合はこの機会に覚えて、クイズとしてまわりに出題してみてくださいね!
りんごのイラスト/タワシ
※一部、AI生成画像を使用しています。














.png)
